|
XYZ-Wing
Points.
The XYZ-Wing is an extension of the XY-Wing and
like the XY-Wing, it uses 3 digits named X, Y and Z. The XYZ-Wing has three
cell truths. The center cell is called the pivot with 3 candidates XYZ, the
other 2 cells are called pincers and contain XZ and YZ. Any cell that can
see both pincers cannot contain another candidate for digit Z. What Sudopedia says.
|
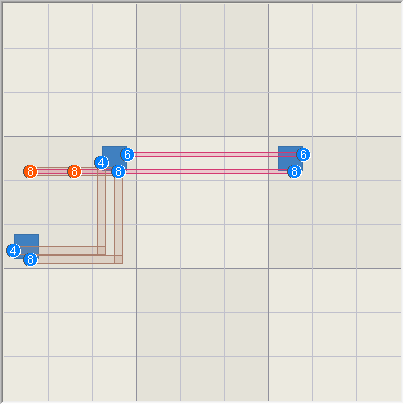
XYZ-Wing Theory. The
example on the right is a theoretical drawing of an XYZ wing showing the
three cells and two possible eliminations. The pivot cell is r4c3 and
contains the digits 4, 6 and 8. The two 8s are eliminated because they both
see the 8s in the two pincer cells.
Reasoning by truths and
covers, 3 truths are covered by 4 covers thus anywhere 2 covers overlap
will eliminate candidates.
|
|
|
XYZ-Wing Example 1. The
XYZ-Wing on the right has a pivot cell in r8c5 with digits 1, 6, and 7. The
red candidate (1)r7c5 sees both the 1s in r2c5 and r9c4 and is thus eliminated.
Reasoning by truths and
covers, 3 truths are covered by 4 covers thus anywhere 2 covers overlap
will eliminate candidates.
|

|
|
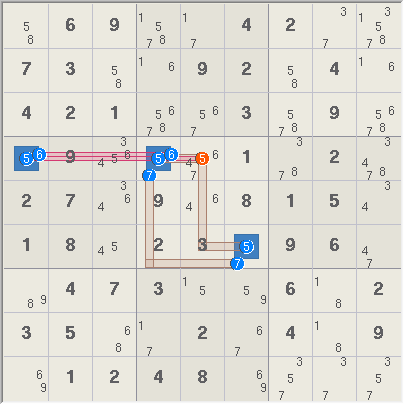
XYZ-Wing Example 2. The
XYZ-Wing on the right has a pivot cell in r4c4 with digits 5,6,7. The red
candidate (5)r4c5 sees both the 5s in r4c1 and r6c6 and is thus
eliminated.puzzle.
|
|
|
XYZ-Wing Example 2. The
3D view of example 2 clearly shows both pincer cells double linked to the
pivot cell.
|

|
|
|
XYZ-Wing Example 2,
Logic Diagram.
Note:
Elimination cadidate is red, candidate 5r4c4 (A) is in 2 cover sets.
(7b5) (5b5) (5r4) (6r4)
4N4: 7r4c4==5r4c4A=5r4c4A=6r4c4
| | | |
6N6: 7r6c6==5r6c6 | |
| | |
4N1: | 5r4c1==6r4c1
| |
\ /
5r4c5
|



