|
WXYZ-Wing
Points.
The WXYZ-Wing is an extension of the XYZ-Wing that
has four cells, a pivot cell with digits WXYZ and three pincer cells
with digits WZ, XZ and YZ. Any cell that sees all Z
candidates in the WXYZ-Wing cannot contain another candidate for digit Z.
There are many extended WXYZ-Wing types with different configurations and
numbers of candidates in each cell. The two primary types are shown below as
theoretical drawings. All types are logically the same in terms of truths and
covers. WXYZ-Wings can also be considered using ALS. What Sudopedia says.
|
WXYZ-Wing Theory, basic. The
example on the right is a theoretical drawing of the most basic WXYZ-Wing form.
The pivot cell is r5c2 and contains four digits 2, 4, 6 and 8. The two 8s
int r4c12 are eliminated because they both see the 8s in the the pincer
cells.
Reasoning by truths and
covers, 4 truths are covered by 5 covers thus anywhere 2 covers overlap
will eliminate candidates.
|

|
|
WXYZ-Wing Theory, extended type 1. The example on the right is a theoretical drawing of
an extended type 1 WXYZ-Wing. It has additional candidates in the two
pincer cells in row 4, columns 5 and 8.
|
|
|
WXYZ-Wing Theory, extended type 2. The example on the right is a theoretical drawing
of an extended (type 2) WXYZ-Wing. The extended type 2 form has two pincers
in the box both of which have 3 candidates.
|

|
|
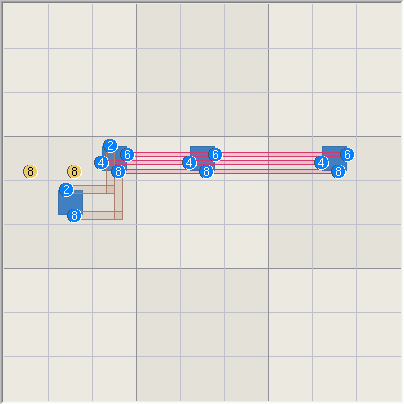
WXYZ-Wing, Extended Example 1. The
WXYZ-Wing on the right is similar to the type 1 extended form, except two
cells overlap in the box/line intersection.
|
|
|
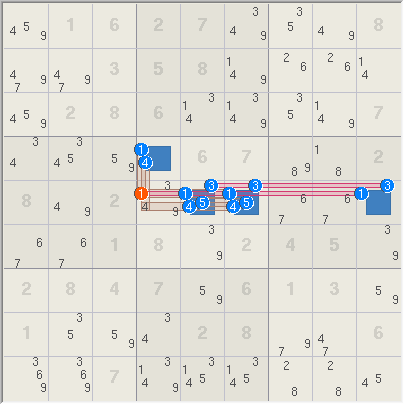
WXYZ-Wing, Extended Example 2. The
WXYZ-Wing on the right has no single cell with all four of the WXYZ
candidates. Although not always considered as a WXYZ-Wing however, it works
exactly the same way.
|

|
|




