Turbot Fish. The first turbot fish example is also a vertical skyscraper, which works like a very simple chain. The cover link regions are highlighted showing the overlap region between box 1 and row 2.

In terms of implications:

9r2c7  => r2c3<>9

r2c7<>9 => 9r8c7 => r8c2<>9 => 9r2c2 =>  r2c3<>9

In terms of truths and covers, 2 truths + 3 covers imply any candidate covered by two links can be eliminated. Thus r2c3<>9.  The elimination region includes all three cells in the intersection of box 1 with row 2.

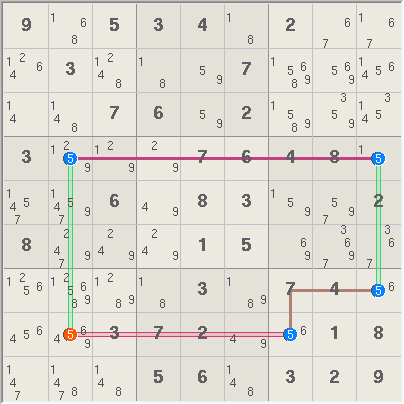
Box/row Turbot Fish. This turbot fish again works like a very simple chain. It is different from the first example becasue it uses a box truth and a row truth.

In terms of truths and covers, 2 truths + 3 covers imply any candidate covered by two links can be eliminated. Thus r8c2<>5. 

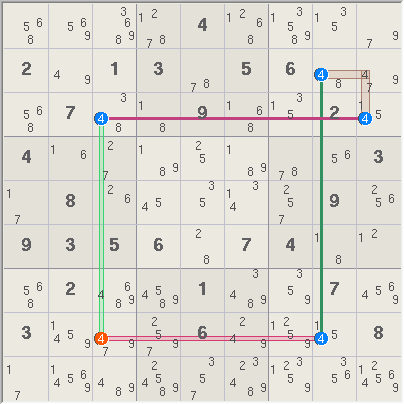
Row/Column Turbot Fish. Example 3 is both a Turbot Fish and a Crossed Two String Kite.  It uses a row truth and a column truth.

In terms of truths and covers, 2 truths + 3 covers imply any candidate covered by two links can be eliminated. Thus r8c3<>4. 

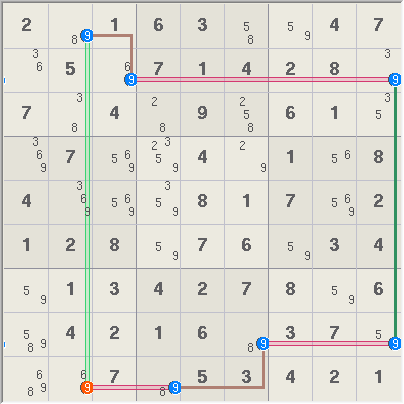
Length 7 Turbot Fish. A Turbot Fish with a length of 7 is made of 3 truths and 4 cover links. This pattern is also known as a Fishy Cycle.

In terms of truths and covers, 3 truths + 4 covers imply any candidate covered by two links can be eliminated. Thus r9c2<>9. 

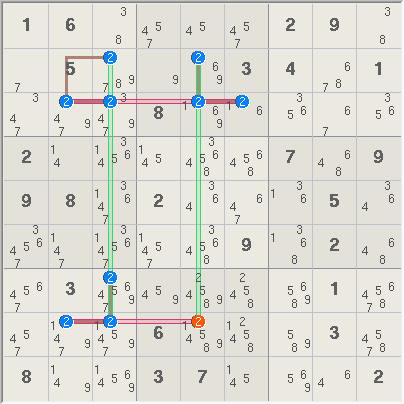
Fully Grouped Turbot Fish. A Turbot Fish with a length of 7 is made of 3 truths, all of which are boxes, and 4 cover links. All of the six connections between truths and covers are grouped, using more than 1 candidate.

The logic is again simple in terms of truths and covers, 3 truths + 4 covers means a rank of 1 thus any candidate covered by two links can be eliminated. Thus r8c5<>2.