|

|
Points. A logical solution to Golden Nugget gives insight into the nature
of extreme puzzles. The solution uses a freeform logic that can assume any
form. Many of GN's eliminations tkae the form of layered single digit
patterns that connect vertically through common groups of linksets.
|

|
Golden Nugget
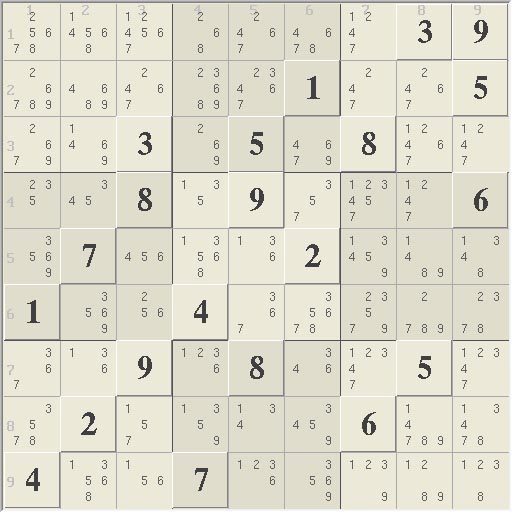
The Solution
Golden Nugget is without a doubt a difficult puzzle.
This set logic solution provides perhaps a different way of viewing the logic
inside of the puzzle as compared to other methods. Below is a chart that
shows the relative difficulty of each move based on (blue) the number of sets
used by the logic and (red) the number of nodes involved in the logic. Most
difficult moves require around 20 - 25 sets and roughly 70 nodes. A few
eliminations have some broken wing logic, which uses a relatively higher
number of sets. The most difficult eliminations fall into 3 groups of 10 to
15 eliminations where each group is followed by an assignment. These
assignments roughly correlate to the gaps between the 3 groups.
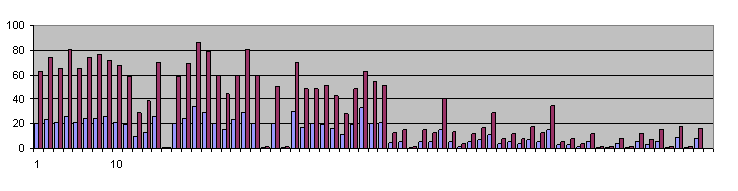
Like the solution to Easter
Monster, the solution to Golden Nugget uses a freeform logic that can
take on most any form. The first thing apparent from the solution is that
many difficult eliminations are well beyond any simple interpretation using
set logic rules.
However, a number of interesting exceptions take the
form of 4 or 5 single digit layers connected through a single group of
vertical linksets. Each layer forms a strong inference set (SIS) that
combines with other SIS in the vertical linksets to cause eliminations. In
some cases, one layer receives the combined effect of the other layers and in
one case, the SIS fill the vertical linksets until they become rank 0 and
cause eliminations. Such highly organized logic is suprising and may indicate
a logical weakness in this monster. (Note: the solver works based on sets and
permutations without using rules like rank, cover sets, or alternating
strong-weak links, any organized structure is what the solver considered easy
to find.)
The table at the bottom of the page gives links
to set logic and diagrams for all
eliminations. The thumbs in two tables below link to specific eliminations
that have been studied in more detail, which will be added to as more are
analyzed.
Early Eliminations
|
|

|
|
|
Layer Cake
E1. Five single digit layers combine 5 strong
inference sets to make rank 0 logic.
|
The Worst
E16. The worst elimination required 65 sets +
linksets and eliminates two candidates.
|
Negative
Inference Set
E19. Three layers form 3 strong inference sets
that combine into a 4th layer.
|
The Tail End
|

|

|
|
|
Simple
Proof
E10. An example of a simple set logic proof for
moderately complex logic.
|
Simple Proof
E64. A second example of a simple proof with set
logic.
|
One Rank 0
Linkset
E39 uses one elimination to build the logic for a
second elimination. No analysis.
|
|
|
|
|
|
In the
shadow of triplets
E44. Rank 0 logic with several triplets that can
raise rank, but not at the elimination.
|
Rank 4 + 3
Triplets
E23x. Rank 4 example with 3 triplets to lower rank
to 1 for an elimination.
|
Helicopter
E49. Simple Rank 2 ALS and chain
example with triplet.
|
|
|
|
|
|
EX51
E51x True to life, this simple 18 sided bi-value
nice loop shows
|
Nowhere Loop
E64. True to life, this simple 18 sided bi-value
nice loop shows how hard it is to get anywhere.
|
Final
Breakup
E67. The final breakup of
GN's logic.
|
List of Links to Eliminations 1 -
67
|
G01a,
grid[21.242] 58 sets s2:0 p136 p793
|
G33a,
grid[23.196] 53 sets s1:0 p571
|
|
G01b,
grid[21.242] 38 sets s1:0 p793
|
G34a,
grid[23.195] 46 sets s1:0 p672
|
|
G02a,
grid[21.240] 47 sets s1:0 p743
|
G35a,
grid[23.194] 43 sets s2:0 p277 p367
|
|
G03a,
grid[21.239] 58 sets s1:0 p246
|
G36a,
grid[23.192] 11 sets s1:0 p791
|
|
G04a,
grid[21.238] 47 sets s1:0 p217
|
G37a,
grid[23.191] 11 sets s2:0 p392 p982
|
|
G05a,
grid[21.237] 54 sets s1:0 p443
|
G38a,
grid[23.189] 3 sets s1:0 p472
|
|
G06a,
grid[21.236] 61 sets s1:0 p284
|
G39a,
grid[23.188] 13 sets s1:0 p252
|
|
G07a,
grid[21.235] 51 sets s1:0 p242
|
G39b,
grid[24.128] 12 sets s1:0 p252
|
|
G08a,
grid[21.234] 50 sets s1:0 p366
|
G40a,
grid[23.188] 31 sets s1:0 p463
|
|
G09a,
grid[21.232] 46 sets s1:0 p797
|
G41a,
grid[23.186] 13 sets s2:1
|
|
G09b,
grid[21.232] 56 sets s1:0 p282
|
G42a,
grid[24.180] 4 sets s1:0 p156
|
|
G10a,
grid[21.230] 20 sets s1:0 p236
|
G43a,
grid[24.179] 13 sets s1:0 p953 ]
|
|
G11a,
grid[21.229]30 sets s1:0 p226
|
G44a,
grid[24.177] 14 sets s1:0 p546
|
|
G12a,
grid[21.228] 53 sets s2:1 p287 p386 a286
|
G45a,
grid[24.176] 24 sets s1:0 p774
|
|
G13a,
grid[21.227] 2 sets s2:1 p216 p256
|
G46a, grid[24.175] 8 sets s1:0 p864
|
|
G14a,
grid[22.223] 43 sets s1:0 p177
|
G47a,
grid[24.174] 9 sets s1:0 p594
|
|
G15a,
grid[22.222] 55 sets s1:0 p972
|
G48a,
grid[24.173] 9 sets s1:0 p766
|
|
G16a,
grid[22.221] 65 sets s1:0 p126
|
G49a,
grid[24.172] 16 sets s1:0 p474
|
|
G17a,
grid[22.220] 61 sets s1:0 p692
|
G50a,
grid[24.171] 13 sets s1:0 p124
|
|
G18a,
grid[22.219] 44 sets s1:0 p772
|
G51a,
grid[24.170] 31 sets s2:1 p677 p717 a777
|
|
G19a,
grid[22.218] 32 sets s1:0 p142
|
G52a,
grid[25.163] 7 sets s1:0 p425
|
|
G20a, grid[22.217] 48 sets
s1:0 p319
|
G53a,
grid[26.154] 8 sets s4:2 p171 p741 p831 p931
|
|
G21a,
grid[22.216] 60 sets s1:0 p212
|
G54a,
grid[28.143] 4 sets s2:0 p384 p394
|
|
G22a,
grid[22.215] 44 sets s1:0 p248
|
G55a,
grid[28.142] 10 sets s3:2 p112 p817 a117
|
|
G23a,
grid[22.214] 2 sets s2:0 p118 p128
|
G56a[31.133]
2 sets s2:0 p384 p884
|
|
G24a,
grid[22.212] 40 sets s3:1 p224 p249 p253 a243
|
G57a[31.131]
2 sets s1:0 p394
|
|
G25a,
grid[23.206] 2 sets s1:0 p329
|
G58a[31.130]
9 sets s1:0 p663
|
|
G26a,
grid[23.205] 60 sets s2:0 p116 p346
|
G59a[31.129]
2 sets s1:0 p853
|
|
G27a,
grid[23.203] 41 sets s1:0 p516
|
G60a[31.128]
13 sets s1:0 p991
|
|
G28a,
grid[23.202] 45 sets s1:0 p134
|
G61a[31.127]
7 sets s1:0 p963
|
|
G29a,
grid[23.201] 43 sets s2:0 p921 p925
|
G62a[31.126]
13 sets s3:0 p665 p951 p966
|
|
G30a,
grid[23.199] 37 sets s1:0 p535
|
G63a[31.123]
2 sets s2:0 p881 p891
|
|
G31a,
grid[23.198] 25 sets s1:0 p164
|
G64a[31.121]
18 sets s1:0 p553
|
|
G32a,
grid[23.197] 43 sets s1:0 p382
|
G65a[31.121]
2 sets s1:0 p845
|
|
G66a[31.120]16 sets s3:3 p397
p591 p698 a387 a391 a697
|
|
G67a [End] 25 sets s16:10 p146
p312 p326 p349 p424 p548 p588 p593 p623 p688 p716 p869
|
Notes
For more information about
notation and how set logic works see Quick Guide to
Sudoku Set Logic. To look for specific Sudoku examples, go back to the Homepage.
|














