|
A General Sudoku Logic Easter Monster |
Easter Monster Easter Monster wins the prize for beauty and
elegance with a wide variety of difficult and medium level moves that illustrate
various logical principles. Example eliminations are shown and discussed here
and the rest can be seen by clicking on the list of eliminations at the
bottom of the page. Some smaller but interesting eliminations are presented,
rather than focusing on the most difficult. For difficulty, see number 8
below.
The solution The solution to Easter Monster is based on freeform logic that allows eliminations to assume any form. The logic should therefore be more natural than logic produced by techniques that require specific logical forms. For example, freeform logic never requires more than about 60 nodes for the most difficult eliminations. General set logic theory provides relatively simple explanations for these eliminations. In fact, the most difficult eliminations rely more heavily on the two main principles of general set logic, 1) the containment of eliminatees in multiple sets and 2) the use of triplet links to "concentrate" the logic. Unlike
the relentless single candidate eliminations in Top1465 #77, Easter Monster
mixes multiple eliminations, very difficult single eliminations, and an
interesting variety of medium level logic. A Note on Notation Eliminations are written in standard notation except
for sets, which are written in a form that makes them easy to recognize. The
notation follows the definition of Sudoku sets in 3D, and adds an extra
number so that row 4 contains row sets r41 to r49. The extra number is the
digit except for cell sets, which are noted by row and column. The four types
of sets are then: row = R(row, digit),
column = C(column, digit), cell = N(row, column), box = B(box, digit) Subgroups like c51, c53, and c59 are written as
c5(139). The short notation is meant for use with diagrams that provide exact
candidate details. However, set theory says that all eliminations can be
understood based on sets alone without candidate details, in principle. A example elimination expression is: Rank 1: [r46 c5(139) c76 n23
n3(12)](ST) r26*c56 => r2c5
<> 6. which is of the form: <rank>:
[list of covering sets](triplet info)<overlap linksets> =>
<assignments>,<eliminations> In some cases
<overlap linksets> is replaced with [list of covering linksets],
particularly for rank 0 logic (like fish) where all linksets can cause
eliminations. The triplet information
denotes the presence of triplets, where T means a linkset Triplet
and S means a Set triplet. Quick Description of Sudoku Set
Logic The following is a quick description of how Sudoku
set logic can be applied to complex logic however, it is not a complete set
guide rules. I hope to have such a set of rules soon. 1. Every solution is based on two groups of
sets. The [b]set[/b] group exactly contains a group of candidates and the
[b]linkset[/b] group contains these candidates as well as other candidates
that are potential eliminations. 2. The number of linksets minus the number of
sets is called rank, which relates to missing constraints. Rank is a
distributed property of the logic and applies everywhere within a logical
structure except for conditions noted below. 3. Rank 0 eliminates any additional
candidates inside of linksets. Common examples include singles, locked candidates,
ALCs, X-wing, swordfish, etc. 4. Rank 1 eliminates any additional
candidates where two linksets overlap. Many Sudoku methods fall into this
category such as finned fish, chains, discontinuous nice loops, etc. 5. Ranks 2 (or 3) logic requires 3 (or 4)
simultaneously overlapping linksets to cause eliminations. 6. Ranks higher than 3 can only cause
eliminations when combined with [b]triplets[/b], described next. 7. A triplet is a single candidate that
connects three sets. A set-triplet has two sets and one linkset, and a
linkset-triplet has two linksets and one set. Triplets "point" in
the direction of the minor link, i.e., the linkset direction of a two set
triplet. The two types of triplets are similar but have different properties. 8. Triplets can divide logic into high rank
and low rank regions and therefore change the number of linksets that are
needed to eliminate a candidate, but this must follow specific rules. When
linkset triplets point in the direction of a candidate, it may reduce the number
of linksets required to eliminate the candidate. 9. Set triplets can increase the number of
overlap linksets required to make an elimination if they reduce the number of
true nodes (assigned candidates) guaranteed to be in the set group.
Link-triplets cannot. 10. The candidate in a set-triplet with an
unconnected linkset can be assigned in rank 0 logic. 11. When triplets are located and aligned
correctly, their effects can be additive however, complex arrangements often
require consideration or additional logical analysis. 12. When two blocks of logic are
(hypothetically) combined, each retains its original rank internally and the
rank of the combined logic is the sum of the
individual ranks. Eliminations can occur when linksets of different
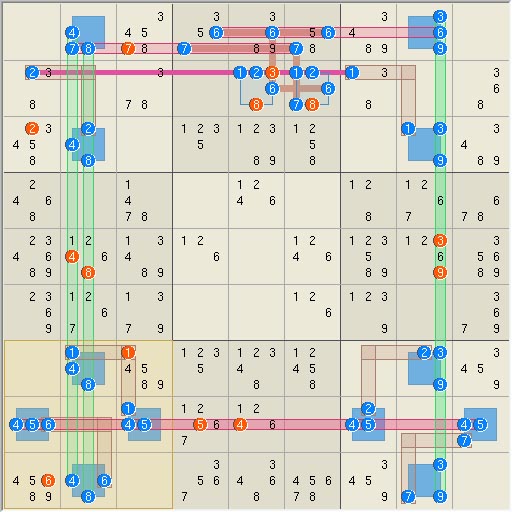
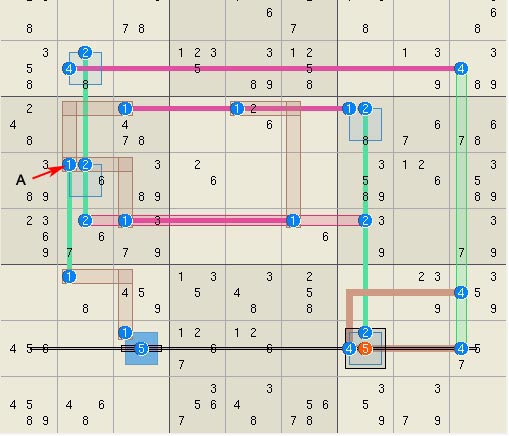
blocks overlap based on the overall rank and triplets used to link blocks. Elimination 0, rank 0 super fish. The first and
one of the most interesting eliminations has been reported previously and the
logic is shown here. The highly
symmetric solution can take many forms, all of which use 16 sets and 16
linksets to make a ring like rank 0 super-fish that eliminates 13 candidates.
Because it is a rank 0 closed loop, general Sudoku set theory classifies it
in the same category as an X-wing. Rank 0, S[r2(12) n1(28) n3(28) n7(28) n8(1379)
n9(28) b2(67)], L[r1(67) r8(45) c2(48) c8(39) n2(56) b12 b31 b7(16) b9(27)]
=> r1c3<>7, r2c5<>3,
r2c5<>8, r2c6<>8, r3c1<>2, r5c2<>4, r5c2<>8,
r5c8<>3, r5c8<>9, r7c3<>1, r8c4<>5, r8c5<>4, r9c1<>6 which is of the form
S[set group]+L[linkset group] => <eliminations>
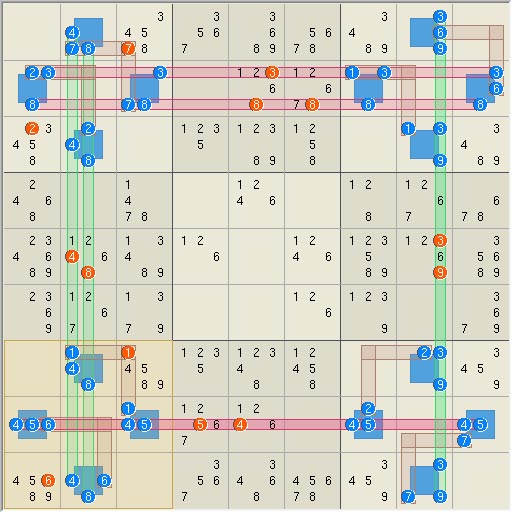
Another version of
the same elimination is shown here.
This solution is more symmetrical and uses only cell sets in the four
corner boxes Rank 0,
S[n1(28) n2(1379) n3(28) n7(28) n8(1379) n9(28)], L[r2(38) r8(45)
c2(48) c8(39) b1(27) b3(16) b7(16) b9(27)] => r1c3<>7, r2c5<>3,
r2c5<>8, r2c6<>8, r3c1<>2, r5c2<>4, r5c2<>8,
r5c8<>3, r5c8<>9, r7c3<>1, r8c4<>5, r8c5<>4,
r9c1<>6
Eliminations 2 to 4, rank 0
symmetric Naked Triples. Eliminations 2
and 4 are row and column naked triples symmetrically arranged in a '+'
pattern centered in the middle of the grid. They fill the gaps in the
structure of elimination 1. Together they remove another 15 candidates and
produce the first assignment, elimination 2, which removes 6 more candidates. Elimination 1: Rank 0,
S[n5(248)] + L[r5(126)] => r5c1<>2,
r5c1<>6, r5c3<>1, r5c6<>1, r5c6<>2, r5c6<>6,
r5c7<>1, r5c7<>2, r5c9<>6
Elimination 3. Rank 0,
S[n56](single) => r5c6=4,
r4c5<>4, r5c1<>4, r5c3<>4, r7c6<>4,
r9c6<>4. Elimination 4. Rank 0,
S3=[n(248)5] + L[c5(126)] =>
r1c5<>6, r3c5<>1, r3c5<>2, r7c5<>1,
r7c5<>2, r9c5<>6.
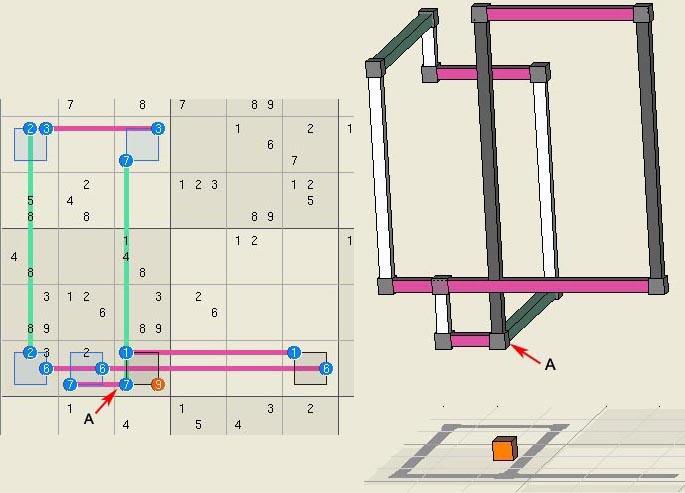
Elimination 23, a triplet
jellyfish. Elimination 23
is s simple example of a set triplet.
This structure
would be a rank 0 jellyfish with 4 sets and 4 linksets except that Rank 0, [c(357)1 b51] +
[r(2468)1](S) => r4c8<>1
Elimination 10, rank 2 triplet
Kraken fish. Elimination 10
is a single digit example of a linkset triplet Kraken fish.
Elimination 10
has 4 sets connected by 6 linksets and is therefore rank 2, which requires 3
overlapping linksets to however, there is no place where this happens.
According to set logic rules, the minor side of triplet A has a rank that is
lower by 1 this rank = 1. Column 9 and row 6 can therefore overlap and remove
candidate r6c9n6. The region of lower
rank caused by triplet A is highlighted in crimson (or yellow for column 9).
The logic is then: Rank 2, [r(28)6 c26
b56](T)r56*c96 => r6c9<>6
Elimination 26, simple logic.
Elimination 26
is a medium size rank 2 cluster but its logic is simple. It needs 3
overlapping linksets to make elimination but has only two. The only triplet A
lowers the rank along the path with cell set n83 thereby allowing overlapping
linksets r85 and n87 to eliminate candidate r8c7n5. The point being that the
complexity of the rest of the logic is not relevant according to general set
logic. Rank 2, [r(46)1 r34 c2(12) c72 n83 b94](T)r85*n87
=> r8c7 <> 5
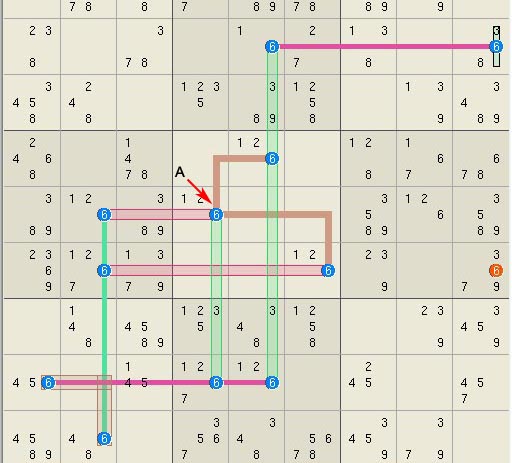
Elimination 62, Twisted loop
solved by set triplet.
Elimination 62
forms a rank 0 double loop with 6 sets and 6 linksets. One of the joints is a
set triplet that lowers the effective rank to 1. The minor side of triplet A
starting with cell set n63 is rank 0 allowing the candidate r6c6n9 to be
eliminated. The notation for the elimination is: Rank 0, [r23 r6(167) c12 c37](S)n63 => r6c3<>9 Elimination 32, a rank 0 path in a
rank 1 group.
Elimination 32
is a rank 1 multiple-loop with both set and linkset triplets. Although it has
7 sets, only 6 true nodes are guaranteed if set triplet S is occupied
and the effective rank for the structure would be 2. However, set triplet S
points in the direction of row 51 and lowers the rank along that path.
Linkset triplet T points in the opposite direction along the same path
lowering the effective rank further to rank 0. Linksets along this path can
therefore eliminate candidates including the one at r5c9n5. This illustrates
the additive nature of triplets. The rank 0 sets are highlighted in black.
The elimination is thus: , S7=[r35 r51 c35
c82 n7(26) b71](ST)n58 =>
r5c8<>6
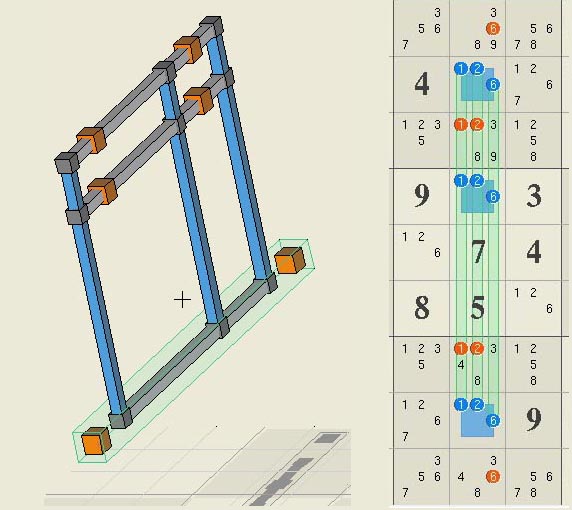
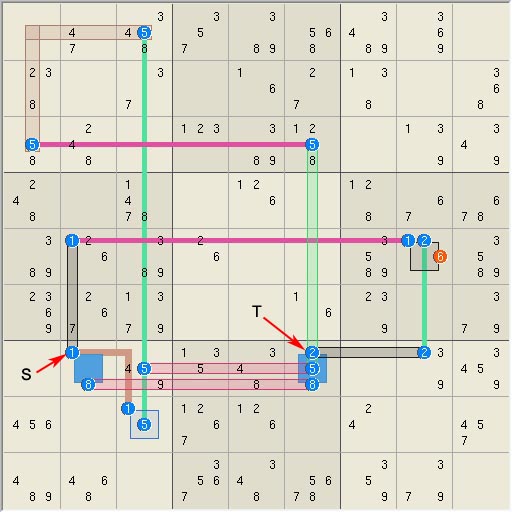
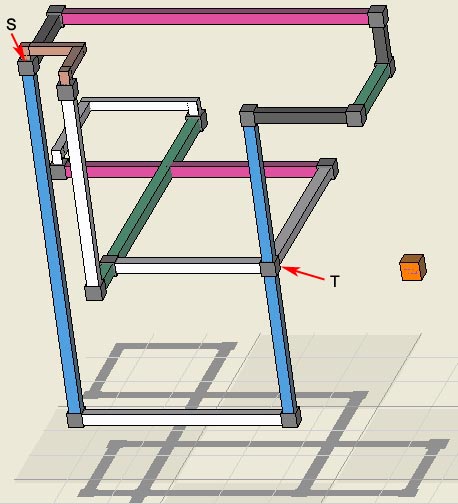
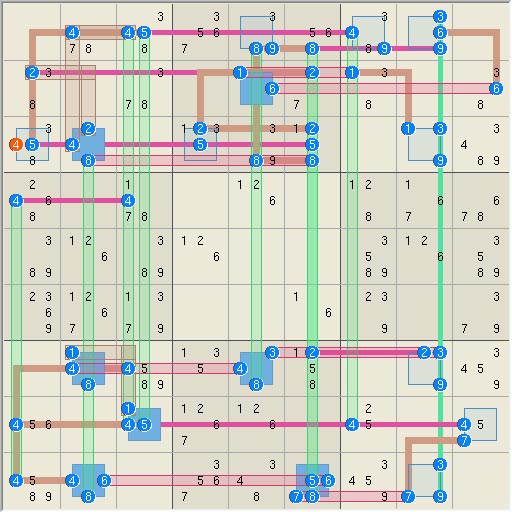
Elimination 8, rank 6 logic! Last but surely
not least is elimination 8, which has the incredible rank of 6, which implies
that 7 overlapping linksets are required to eliminate a candidate. The logic
is small relative to other difficult eliminations and uses only 15 sets plus
required linksets.
As shown in the
logic diagrams, candidate r2c5n2 sits at the intersection of 4 link sets
however, this is not enough to eliminate the candidate. The three linkset
triplets marked as A, B, and C all point in the
direction of the candidate and thus lower the effective rank in the region of
the candidate. Such effects are usually additive. Set triplets, most
obviously X and Y, are also oriented correctly in the direction
of the candidate. A proper analysis of multiple triplets is not difficult but
the final proof is that the candidate is eliminated. S15=[r21 r34 r4(247) c(58)1
c(168)2 n8(39) b1(25) b62], L21=[r(48)1 r(267)2 r85 c3(45) c72 c9(47) n25
n3(12) n4(1358) n58 b22 b31] =>
r2c5<>2 .
Elimination 14, the bigger the
better, 51 set logic cluster.
Elimination 14 is
the largest set cluster found while solving Easter Monster. It is a rank 5
structure with 51 sets and many triplets. The 51 sets contain 61 candidates.
The set notation for the structure is: Rank 5, [r(27)2 r(148)4 r35
r19 c8(39) n(379)2 n83 n(27)5 n96 b15 b2(28) b3(16) b74 b97] + [r2(16) r38
r7(34) r9(67) c14 c28 c3(45) c58 c6(258) c74 n31 n34 n15 n17 n(1379)8 n89
b1(24) b71] => r3c1<>4.
Grids and images for all
eliminations The following list contains all eliminations except for those due to singles. Grids and images for the elimination can be seen by clicking on the elimination summary. Initial Rank 0 Eliminations clear 34 candidates. 1.Giant rank 0 loop eliminates 13, S16=[r2(12) n1(28) n3(28) n7(28) n8(1379)
n9(28) b2(67)], L16=[r1(67) r8(45) c2(48) c8(39) n2(56) b12 b31 b7(16)
b9(27)] => r1c3<>7,
r2c5<>3, r2c5<>8, r2c6<>8, r3c1<>2, r5c2<>4,
r5c2<>8, r5c8<>3, r5c8<>9, r7c3<>1, r8c4<>5,
r8c5<>4, r9c1<>6 1a.
Giant rank 0 loop eliminates 13, take II,
S16=[n1(28) n2(1379) n3(28) n7(28) n8(1379) n9(28)], L16=[r2(38) r8(45)
c2(48) c8(39) b1(27) b3(16) b7(16) b9(27)] => r1c3<>7, r2c5<>3,
r2c5<>8, r2c6<>8, r3c1<>2, r5c2<>4, r5c2<>8,
r5c8<>3, r5c8<>9, r7c3<>1, r8c4<>5, r8c5<>4,
r9c1<>6 2.
Naked Triples, row 5. S3=[n5(248)], L3=[r5(126)]
=> r5c1<>2, r5c1<>6,
r5c3<>1, r5c6<>1, r5c6<>2, r5c6<>6, r5c7<>1,
r5c7<>2, r5c9<>6 3.
First Single. S1=[n56], L0=[] => r5c6=4, r4c5<>4, r5c1<>4,
r5c3<>4, r7c6<>4, r9c6<>4 4. Naked Triples, column 5. S3=[n(248)5],
L3=[c5(126)] => r1c5<>6,
r3c5<>1, r3c5<>2, r7c5<>1, r7c5<>2, r9c5<>6 Difficult Region. 5.
Large 46 set cluster embedded 9 set strong loop .
S23=[r2(23678) r41 r52 c(68)1 c(268)2 n1(278) n25 n47 n58 b(27)1 b12 b36
b47], L23=[r(367)1 r(37)2 r14 r19 c3(17) c51 c78 c86 n2(1369) n62 b1(78) b33
b52 b6(12)] => r6c7<>1 6.
Medium 28 set cluster, embedded 9 set strong loop,
S17=[r2(267) r56 r71 c(457)1 c22 c(58)6 c27 n25 n52 b12 b3(16)], L11=[r(234)1
r46 c21 n26 n54 n62 n85 b17 b81] =>
r2c6<>1 7.
Rank 5 large 44 set cluster, S19=[r21 r(35)2
r(378)4 r56 r78 c15 c24 c5(126) n83 n92 b61 b(89)2 b76], L24=[r8(126) c71
c(248)2 c94 c26 n31 n32 n54 n(247)5 n76 n87 n(45)8 b14 b22 b7(458)]
=> r4c8<>2 8.
Rank 6 medium 35 set cluster, S15=[r21 r34 r4(247)
c(58)1 c(168)2 n8(39) b1(25) b62], L20=[r(48)1 r(2367)2 r85 c3(45) c52 c9(47)
n25 n3(12) n4(138) n58 b31] =>
r2c5<>2 9.
Rank 1, Two linked nice loops collide, S8=[r2(27)
c2(27) n25 n58 b3(16)], L9=[r2(16) r52 c8(16) n26 n62 b1(27)] => r2c6<>6 10.
Rank 2, Small one digit pattern needs triplet.
S4=[r(28)6 c26 b56], L6=[r(56)6 c(459)6 b76] => r6c9<>6 11.
Rank 4, blue-green 30 set forest, S13=[c3(17) c52
c7(12) c9(67) n2(56) n4(58) n54 n84], L17=[r(248)1 r(68)2 r(24)6 r(2468)7 c46
c62 n47 n63 b5(12)] =>
r6c6<>2 12.
Medium 35 set cluster. S18=[r(235)1 r(38)2 c(458)1
c56 n(56)2 b31 b52 b6(267) b7(16)], L17=[r52 r67 r8(16) c21 c(2457)2 c26 n25
n36 n4(589) n58 n74] =>
r7c4<>2 13.
Medium cluster with embedded 5 set strong loop,
S14=[r6(16) r96 c(2569)6 c(24)7 n26 b46 b71 b8(12)], L13=[r71 r(24)6 r17 c31
c62 n16 n6(26) n8(45) n94 b27] =>
r1c6<>7 14.
Rank 5, the largest, 51 set, cluster. S23=[r(27)2
r(148)4 r35 r19 c8(39) n(379)2 n83 n(27)5 n96 b15 b2(28) b3(16) b74 b97],
L28=[r2(16) r38 r7(34) r9(67) c14 c28 c3(45) c58 c6(258) c74 n31 n34 n15 n17
n(1379)8 n89 b1(24) b71] =>
r3c1<>4 15.
Rank 1 multi-loops with set triplet 17 sets,,
S8=[r2(27) c35 n81 n(139)2 b14], L9=[c2(48) n13 n26 b1(27) b7(456)]
=> r7c2<>4 16.
Rank 3 large 41 set cluster, 3-linkset overlap.
S19=[r17 r3(249) r87 r97 c24 c5(349) c6(16) n1(578) n26 n72 n98 b28],
L22=[r1(3689) r71 r9(34) c(46)7 c28 c89 n12 n3(2569) n66 n75 n96 b22 b34 b97]
=> r1c2<>8 17.
Rank 3 medium 39 set cluster, 3 linkset overlap,
S18=[r(34)4 r79 c13 c28 c35 c82 n31 n(124)3 n26 n(68)9 b12 b48 b6(17)],
L21=[r2(27) r4(17) r63 r85 c3(48) c9(479) n32 n41 n5(18) n7(38) b1(358) b78]
=> r7c3<>8 18. Dense 41 set cluster,
embedded strong loop. S22=[r14 r27 r3(25) r61 r81 r95 c15 c2(2467)
c4(267) c6(25) n6(26) n8(47) b25], L19=[r52 r8(25) c(36)1 c74 n(159)2 n(19)4
n(237)6 b1(47) b56 b81 b95] =>
r7c6<>1 19.
Bi-value box ended chain. S5=[r66 c61 c96 n25 n66],
L4=[r(24)6 b21 b46] =>
r4c1<>6 20.
Multi-loop Kraken like structure, 13 sets.
S6=[r2(27) c2(27) n66 b46], L7=[r6(16) n(56)2 n26 b1(27)] => r6c2<>1 21.
Triple inter-connected broken wing like strong loops.
S18=[r(258)1 r46 r87 c(358)1 c87 n4(58) n54 n84 b3(16) b41 b52 b97], L4=[r16
c4(26) c96] => r1c4<>6 22.
Rank 6 40 set cluster with 3 overlap linksets and many
triplets. S17=[r46 r7(28) c68 n13 n38 n58 n66 n7(348) n83 b2(135) b71
b81], L23=[r(358)1 r(137)3 r18 r79 c3(45) c4(15) c51 c8(29) n72 n(137)6
b5(16) b66 b88] => r5c4<>1 23.
Simple rank 0 fish with set triplet, S4=[c(357)1
b51], L4=[r(2468)1] =>
r4c8<>1 24.
Large 40 set cluster with embedded strong loops.
S24=[r17 r39 r51 r7(128) c2(14) c43 c67 c8(13) n26 n38 n7(258) n9(58) b23 b34
b8(348)], L16=[r13 r3(34) r9(347) c62 c74 c89 n1(24) n3(59) n74 n96 b27]
=> r9c7<>4 25.
Rank 2 30 set cluster, 2 overlap linksets + 1 triplet =
elimination. S14=[r51 r(17)9 c5(348) c74 c82 c94 n3(189) b7(15)],
L16=[r3(38) r84 c(28)1 c15 n15 n58 n7(3589) n83 n95 b3(49)] => r8c3<>4 Medium Region. 26.
Medium size rank 2, 18 set cluster, simple triplet
example. S8=[r(46)1 r34 c2(12) c72 n83 b94], L10=[r62 r85 c94 n(35)2
n(48)7 b(457)1] => r8c7<>5 27.
Triplets make a rank 0 set in 19 set rank 1 cluster. S9=[r7(125) r85 c21 n83 n(45)8 b97],
L10=[r51 c8(27) c95 n7(46) n89 b66 b7(15)] => r9c1<>5 28.
Rank 1 23 set cluster with 2 set triplets aligned
correctly. S11=[r51 r7(125) r85 c7(58) c82 n87 b34 b61], L12=[c21 c74 n39
n47 n5(78) n7(46) b38 b75 b9(25)] =>
r3c9<>8 29.
Rank 1 hinged Kraken thing, 13 sets. S6=[r1(48) r2(27)
r38 n32], L7=[n17 n2(36) b1(248) b28] =>
r2c3<>8 30.
Rank 3 medium 25 set cluster with triplets.
S12=[r17 r27 r51 r7(12) c(48)3 c59 n2(36) n38 b23], L13=[r(139)3 r39 c(28)1
c62 n1(45) n7(48) b1(37)] =>
r3c1<>3 31.
Rank 1 cluster, 19 sets with one rank 0 set from
triplet. S9=[r61 r72 c15 c94 n3(126) n8(37)], L10=[r3(2458) r85 c31
c6(12) b9(24)] => r3c4<>5 32.
Rank 1 multi-loop with long rank 0 path from triplet to
tripset. S8=[r35 r51 r72 c35 c82 n7(26) b71], L7=[r7(58) c21 c65 n58 n83
b15] => r5c8<>6 Easy Region. 33.
Locked Candidate. S1=[b66], L1=[r46] => r4c5<>6 34.
Small, two string kite. S2=[r56 c16], L3=[r86 c46
b46] => r8c4<>6 35. Bi-Value Chain. S5=[r72 n2(36) n58 b31], L6=[r2(37) c62
c8(12) n27] => r2c7<>3
38. Short nice loop. S3=[r2(237)],
L3=[n2(136)] => r2c1<>8 39. Locked Candidate. S1=[r28], L1=[b38]
=> r1c7<>8 45. Rank 1 bi-value chain. S5=[c21 n58
n83 b9(24)], L6=[r51 r85 c82 n8(79) b71] => r8c9<>5 46. Locked Candidate. S1=[r85], L1=[b75]
=> r7c3<>5 48. Locked Candidate. S1=[b23], L1=[c43]
=> r7c4<>3 49. Nice loop, 8 sets. S4=[r7(28) c21
n58], L4=[r51 c82 n7(26)] =>
r7c6<>5 50. Nice loop, 8 sets. S4=[c56 n16 n81
b15], L4=[r15 r86 c15 b26] =>
r1c4<>5 51. Locked candidates. S1=[c45], L1=[b85]
=> r9c6<>5 52. Bi-value chain.S4=[c67 c8(67) n14],
L5=[r13 r97 n(14)8 b27] =>
r1c8<>3 53.Bi-value chain. S5=[r2(16) c8(12) n18], L6=[c89 n25 n(57)8
b3(16)] => r7c8<>9 54. Small branched loop. S5=[r7(3459)
r95], L6=[c45 n7(359) n97 b93] =>
r9c7<>3 55. Bi-value chain. S4=[c94 n(14)8 b97],
L5=[c8(67) n(38)9 b39] =>
r3c9<>9 57. Locked Candidate. S1=[b67], L1=[r47]
=> r4c3<>7 58. Hidden Pair. S2=[r4(67)], L2=[n4(89)]
=> r4c9<>8 59. Long 12 set nice loop. S6=[c21 c81
c9(58) n27 n74], L6=[r28 r51 r7(15) n59 b31] => r5c9<>9 60. Finned X-Wing. S2=[c(39)9],
L3=[r(67)9 b49] => r6c1<>9 63. Locked Candidates. S1=[r69], L1=[b69]
=> r5c7<>9 65. Single. S1=[n29], L0=[] =>
r2c9=8, r2c7<>8, r5c9<>8 66. Single. S1=[n27], L0=[] =>
r2c7=1, r2c5<>1, r3c8<>1,
r4c7<>1 67. Single. S1=[c81], L0=[] => r5c8=1, r5c2<>1, r5c8<>2 68. Single. S1=[c97], L0=[] => r8c9=7, r8c4<>7, r8c9<>4 69. Single. S1=[c94], L0=[] => r3c9=4, r1c7<>4, r3c2<>4, r3c9<>3 70.Single. S1=[n59], L0=[] =>
r5c9=5, r5c7<>5, r7c9<>5 71. Single. S1=[c82], L0=[] =>
r7c8=2, r7c6<>2, r7c8<>3,
r8c7<>2 72. Single. S1=[c75], L0=[] => r9c7=5, r9c4<>5, r9c7<>9 73. Single. S1=[r85], L0=[] => r8c3=5, r8c3<>1 74. Single. S1=[c21], L0=[] => r7c2=1, r7c2<>8, r7c4<>1 75. Single. S1=[n81], L0=[] =>
r8c1=6, r6c1<>6, r8c5<>6,
r9c2<>6 76. Single. S1=[r84], L0=[] => r8c7=4 77. Single. S1=[r78], L0=[] => r7c6=8, r9c6<>8 78. Single. S1=[r75], L0=[] => r7c4=5 79. Single. S1=[r46], L0=[] => r4c9=6 80. Single. S1=[r26], L0=[] => r2c5=6 81. Locked candidates. S1=[c62], L1=[b22]
=> r3c4<>2 82. 6 set nice loop with box. S3=[c33
n(26)1], L3=[r23 c12 b43] =>
r5c1<>3 83. Medium size nice loop, 10 sets.
S5=[r3(89) r9(89) n15], L5=[c28 c5(89) c89 n91] => r9c1<>4 84. Single. All column nice loop, 8 sets.
S1=[c14], L0=[] => r4c1=4,
r4c1<>8, r4c3<>4 85. All column nice loops. 8 sets, 4 columns.
S4=[c2(67) c4(67)], L4=[r17 r56 n62 n94] => r6c2<>2 86. Twisted nice loop, 10 sets.
S5=[r1(37) r53 r67 n23], L5=[c27 c3(37) c73 n14] => r6c7<>3 Eliminations 87
to 119 are singles. List of Set Groups,
assignments, and eliminations (raw data) The following is a complete list of set and linkset groups for all
eliminations. The form is. 2. S## = [list
of sets in set group], 3. L## = [list
of sets in linkset group] 4. =>
<assigned candidates>, <eliminated candidates>. 2. S1=[n56],
L0=[] => r5c6=4, r4c5<>4,
r5c1<>4, r5c3<>4, r7c6<>4, r9c6<>4 3. S3=[n(248)5],
L3=[c5(126)] => r1c5<>6,
r3c5<>1, r3c5<>2, r7c5<>1, r7c5<>2, r9c5<>6 8. S8=[r2(27)
c2(27) n25 n58 b3(16)], L9=[r2(16) r52 c8(16) n26 n62 b1(27)] => r2c6<>6 9. S4=[r(28)6
c26 b56], L6=[r(56)6 c(459)6 b76] =>
r6c9<>6 14. S8=[r2(27)
c35 n81 n(139)2 b14], L9=[c2(48) n13 n26 b1(27) b7(456)] => r7c2<>4 18. S5=[r66 c61
c96 n25 n66], L4=[r(24)6 b21 b46] =>
r4c1<>6 19. S6=[r2(27)
c2(27) n66 b46], L7=[r6(16) n(56)2 n26 b1(27)] => r6c2<>1 22. S4=[c(357)1
b51], L4=[r(2468)1] =>
r4c8<>1 22. S4=[r(35)1
c(35)1], L5=[r(48)1 c81 b(24)1] =>
r4c8<>1 25. S8=[r(46)1 r34
c2(12) c72 n83 b94], L10=[r62 r85 c94 n(35)2 n(48)7 b(457)1] => r8c7<>5 26. S9=[r7(125)
r85 c21 n83 n(45)8 b97], L10=[r51 c8(27) c95 n7(46) n89 b66 b7(15)]
=> r9c1<>5 28. S6=[r1(48)
r2(27) r38 n32], L7=[n17 n2(36) b1(248) b28] => r2c3<>8 30. S9=[r61 r72
c15 c94 n3(126) n8(37)], L10=[r3(2458) r85 c31 c6(12) b9(24)] => r3c4<>5 31. S8=[r35 r51
r72 c35 c82 n7(26) b71], L7=[r7(58) c21 c65 n58 n83 b15] => r5c8<>6 32. S1=[b66],
L1=[r46] => r4c5<>6 33. S2=[r56
c16], L3=[r86 c46 b46] =>
r8c4<>6 34. S5=[r72
n2(36) n58 b31], L6=[r2(37) c62 c8(12) n27] => r2c7<>3 35. S7=[r61
r(257)2 n45 b1(23)], L8=[c(268)2 c33 n21 n63 b5(12)] => r6c3<>3 37.
S3=[r2(237)], L3=[n2(136)] =>
r2c1<>8 38. S1=[r28],
L1=[b38] => r1c7<>8 41. S7=[r51 c82
n7(2456) n95], L8=[r7(1258) c21 n58 b8(34)] => r9c4<>3 42. S8=[r51 c71
c82 n16 n25 n7(26) b88], L9=[r21 r7(28) c21 c6(58) n58 b26 b61] => r3c6<>8, r9c6<>5 43. S7=[r72 r84 c15
c8(12) n36 n87], L7=[r3(15) c62 n58 n81 b9(24)] => r7c9<>4, r8c1<>4 44. S5=[c21 n58
n83 b9(24)], L6=[r51 r85 c82 n8(79) b71] => r8c9<>5 45. S1=[r85],
L1=[b75] => r7c3<>5 47. S1=[b23],
L1=[c43] => r7c4<>3 48. S4=[r7(28) c21
n58], L4=[r51 c82 n7(26)] =>
r7c6<>5 49. S4=[c56 n16
n81 b15], L4=[r15 r86 c15 b26] =>
r1c4<>5 50. S1=[c45],
L1=[b85] => r9c6<>5 51. S4=[c67
c8(67) n14], L5=[r13 r97 n(14)8 b27] =>
r1c8<>3 52. S5=[r2(16)
c8(12) n18], L6=[c89 n25 n(57)8 b3(16)] =>
r7c8<>9 53. S5=[r7(3459)
r95], L6=[c45 n7(359) n97 b93] =>
r9c7<>3 54. S4=[c94
n(14)8 b97], L5=[c8(67) n(38)9 b39] =>
r3c9<>9 56. S1=[b67],
L1=[r47] => r4c3<>7 57. S2=[r4(67)],
L2=[n4(89)] => r4c9<>8 58. S6=[c21 c81
c9(58) n27 n74], L6=[r28 r51 r7(15) n59 b31] => r5c9<>9 59. S2=[c(39)9],
L3=[r(67)9 b49] => r6c1<>9 60. S5=[r5(26)
r62 n(26)1], L6=[c1(23) n54 b4(26) b62] =>
r4c1<>2 61. S6=[r23
r6(167) c12 c37], L6=[n2(13) n6(1236)] =>
r6c3<>9 62. S1=[r69],
L1=[b69] => r5c7<>9 64. S1=[n29],
L0=[] => r2c9=8, r2c7<>8,
r5c9<>8 65. S1=[n27],
L0=[] => r2c7=1, r2c5<>1,
r3c8<>1, r4c7<>1 66. S1=[c81],
L0=[] => r5c8=1, r5c2<>1,
r5c8<>2 67. S1=[c97],
L0=[] => r8c9=7, r8c4<>7,
r8c9<>4 68. S1=[c94],
L0=[] => r3c9=4, r1c7<>4,
r3c2<>4, r3c9<>3 69. S1=[n59],
L0=[] => r5c9=5, r5c7<>5,
r7c9<>5 70. S1=[c82],
L0=[] => r7c8=2, r7c6<>2,
r7c8<>3, r8c7<>2 71. S1=[c75],
L0=[] => r9c7=5, r9c4<>5,
r9c7<>9 72. S1=[r85],
L0=[] => r8c3=5, r8c3<>1 73. S1=[c21],
L0=[] => r7c2=1, r7c2<>8,
r7c4<>1 74. S1=[n81], L0=[]
=> r8c1=6, r6c1<>6,
r8c5<>6, r9c2<>6 76. S1=[r78],
L0=[] => r7c6=8, r9c6<>8 80. S1=[c62],
L1=[b22] => r3c4<>2 81. S3=[c33
n(26)1], L3=[r23 c12 b43] =>
r5c1<>3 82. S5=[r3(89)
r9(89) n15], L5=[c28 c5(89) c89 n91] =>
r9c1<>4 83. S1=[c14],
L0=[] => r4c1=4, r4c1<>8,
r4c3<>4 84. S4=[c2(67)
c4(67)], L4=[r17 r56 n62 n94] =>
r6c2<>2 85. S5=[r1(37)
r53 r67 n23], L5=[c27 c3(37) c73 n14] =>
r6c7<>3 87. S1=[n34],
L0=[] => r3c4=1, r3c6<>1,
r8c4<>1 88. S1=[n17],
L0=[] => r1c7=9, r1c5<>9,
r3c8<>9, r6c7<>9 89. S1=[n62],
L0=[] => r6c2=6, r5c2<>6,
r6c6<>6 90. S1=[r59],
L0=[] => r5c1=9, r9c1<>9 91. S1=[r63],
L0=[] => r6c1=3, r2c1<>3, r6c1<>2 93. S1=[r67],
L0=[] => r6c3=7, r6c3<>1 94. S1=[r61],
L0=[] => r6c6=1, r4c5<>1 95. S1=[r56],
L0=[] => r5c4=6, r5c4<>2,
r9c4<>6 96. S1=[r52],
L0=[] => r5c2=2, r3c2<>2 97. S1=[r42],
L0=[] => r4c5=2, r8c5<>2 98. S1=[r69],
L0=[] => r6c9=9, r7c9<>9 99. S1=[r74],
L0=[] => r7c5=4, r7c5<>3,
r9c5<>4 100. S1=[r79],
L0=[] => r7c3=9 101. S1=[r81],
L0=[] => r8c5=1 102. S1=[r82],
L0=[] => r8c4=2 103. S1=[r94],
L0=[] => r9c2=4, r9c2<>8 104. S1=[r96],
L0=[] => r9c6=6, r9c6<>7 105. S1=[r97],
L0=[] => r9c4=7 106. S1=[r98],
L0=[] => r9c1=8 107. S1=[r99],
L0=[] => r9c8=9, r9c8<>3 108. S1=[r93],
L0=[] => r9c5=3 109. S1=[c12],
L0=[] => r2c1=2, r2c6<>2 110. S1=[c28],
L0=[] => r3c2=8, r3c5<>8 111. S1=[r73],
L0=[] => r7c9=3 112. S1=[r41],
L0=[] => r4c3=1 113. S1=[r39],
L0=[] => r3c5=9 114. S1=[r33],
L0=[] => r3c8=3 115. S1=[r32],
L0=[] => r3c6=2 116. S1=[r27],
L0=[] => r2c6=7 117. S1=[r23],
L0=[] => r2c3=3 118. S1=[r18],
L0=[] => r1c5=8 To look for specific Sudoku examples, go back to the Homepage. 105.3 |