main page

A General Logic for Sudoku

Monster Loops

Points. Many of the most difficult monster puzzles often have initial highly symetrical loops. Sost of these loops are similar to the original SK loops from EM but many have varying degrees of more complex logic. Ten initial loops are shown from 6 of the most difficult puzzles. .

As more SK type loops emerge, they begin to reveal the nature of the logic inside many great monsters. The original SK loop is large but relatively simple compared to loops from other puzzles like Fata Morgana, Tungsten Rod, and Golden nugget. Golden Nugget is included because its morphed symmetrical form, here reveals similar highly symetrical loops.

The table below summarizes logical properties for 10 loops from 6 top monsters. The puzzles are listed in a subjective order that emphasizes the different kinds of complexity found in the loops. It has been suggested that the central box can play a significant role in the complexity of these loops and 'core' refers to loops with additional logic in the loop's center. Other properties include the presence of bi-value sets, total number of sets used, number of candidates removed, and the logic rank. Rank 0, fish like logic, is common but some puzzles have mixed rank logic that promotes only some links to rank 0. Other properties include symmetric or anti-symmetric digit layers, and layers that have the same or different logic.

These puzzles capture some of the natural beauty of Sudoku logic. While spatial symmetries must be 4-fold, some loops show logical 3-fold symmetries that are both symmetric and anti-symmetric. The most recent loop is Coloin-04/13-1414, rated at 11.8 on the SER scale. The puzzle has two different initial loops, one similar to SteveK's original SK loop from Easter Monster. The other (loop 1) is about the same size, more complex structurally, and wipes out 19 candidates almost solving the puzzle.

Summary Table

------ strong sets -------- remaining

2-value 3-value 4/5-value core logic elim. difficulty

Fata Morgana loop-1 --- 8 3 yes rank 0,1 2

Fata Morgana loop-2 --- 14 - yes rank 0,1 6 medium

Golden Nugget (morph) 1 10 6 yes rank 0,1 1 hard

Tungsten Rod 1 6 2 yes rank 1 2 medium

Coloin-04/13-1414 loop-1 4 11 2 yes rank 0 19 easy

Coloin-04/13-1414 loop-2 2 10 4 no rank 0 14 easy

Easter Monster 4 12 - no rank 0 13 hard

StrmCkr's Puzzle loop-1A 4 12 - no rank 0 9

StrmCkr's Puzzle loop-1B --- --- 12 no rank 0 9

StrmCkr's Puzzle move 2 --- 4 4 yes rank 0 12 v. hard

Logic Diagram Key

123 Candidates in NRC format (digit, row, column)

= Strong set

-|\/ Weak link

A...Z I.e., Letter 'A' notes same candidate in 2 or more sets (triplets)

7C2: Strong let designation, on the left

Note: Logic diagrams omit eliminations for clarity. They are in 2D, 3D images, and set logic.

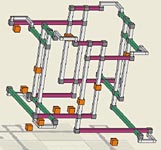
Easter Monster

EM00 44 Nodes, Rank 0:

16 Sets = {1267r2 1267r8 1267c2 1267c8}

16 Links = {2n56 4n8 5n28 6n2 8n45 27b1 16b3 16b7 27b9}

--> (7b1) => r1c3<>7, (2n5) => r2c5<>3, (2n5) => r2c5<>8, (2n6) => r2c6<>8,

(2b1) => r3c1<>2, (5n2) => r5c2<>4, (5n2) => r5c2<>8, (5n8) => r5c8<>3,

(5n8) => r5c8<>9, (1b7) => r7c3<>1, (8n4) => r8c4<>5, (8n5) => r8c5<>4,

(6b7) => r9c1<>6

7C2: 712==762

| |

1C2: | 162==152======================172

| | | |

6C2: | 662==652=================692 |

| | | | |

2C2: | 262==252==232 | |

1R8: | | | 183============185==184

| | | | |

6R8: | | 681=================685==684

2R2: | 221==225==226 | |

| | | | |

1R2: | 125==126=================127 | |

| | | | | |

6R2: | 625==626============629 | | |

| | | | | |

7R8: | | | | | 784=================789

7R2: 723======================726 | | | | |

2R8: | | 285==284==287 |

| | | |

2C8: | | 278==258==248 |

| | | | |

1C8: | 138=================158==148 |

| | | |

6C8: 618======================658==648 |

| |

7C8: 748==798

Image Thumbs

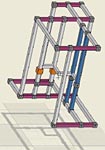
Golden Nugget

GOLD 54 Nodes, Rank 1:

17 Sets = {1247r1 1247r5 1r6 1247r9 6c4 247b5}

18 Links = {27c1 14c2 1247c5 47c8 12c9 145n4 59n6 1b4}

--> (9n6) => r9c6<>3

2B5: 245==========================================256E=254B=244

265 | | |

2R5: | 259==251======================256E=254B |

| | | | | |

2R9: 296=======295============299 | | | |

| | | | | |

2R1: | 214==215=================211 | | |

| | | | |

4B5: | | 445=====================================456F=454C=444

| | 465 | | |

4R5: | | | 452==458============456F=454C |

| | | | | | | |

4R1: | 414=======415=================412 | | | |

| | | | | | |

4R9: 496===|========495======================498 | | |

| | | | |

7B5: | | 745================================756G=754D=744

| | 765 | | |

7R5: | | | 758==751==756G=754D |

| | | | | | | |

7R1: | 714============715======================718 | | | |

| | | | | | |

7R9: 796===|=============795===========================791 | | |

6C4: | | | 654==644

| | | |

1R5: | | 156==154=======152A=152A

| | | |

1R6: | | 162H=162H=165

| | 163 | |

1R9: 196===|====================================================================192==195==199

| | |

1R1: 114========================================================================115==119

Image Thumbs

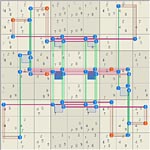
Tungsten Rod

TUNG 28 Nodes, Rank mixed:

9 Sets = {17r2 167r4 17r8 56n6}

13 Links = {1c367 7c367 2n5 4n3457 8n4 5b5}

--> (4n4*5b5) => r4c4<>5, (4n5*5b5) => r4c5<>5

1R2: 126===========================127=================125

| | |

1R8: 186==183=======================|=============184 |

| | | | |

6N6: 566==766==166 | | | |

| | | | | | |

1R4: | | | 143A=143A======145==144==147C=147C | |

| | | | | | | | |

6R4: | | | | 645==644 | | |

| | | | | | | | |

7R4: | | | 743B=743B=745==744=======747D=747D | |

| | | | | | |

5N6: 556==756==156 | | | |

| | | | |

7R8: 786==================|=======================787==784 |

| | |

7R2: 726=================723================================725

Image Thumbs

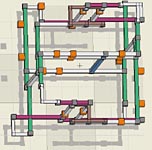
Fata Morgana, Loop 1

FML1 36 Nodes, Rank mixed:

11 Sets = {136c2 136c5 136c8 5n46}

14 Links = {16r1 3r2 136r5 6r8 13r9 4n2 6n8 136b5}

--> (4n2) => r4c2<>2, (4n2) => r4c2<>4

5N4: 154A=====================354B=====================654C

_____/ \_____ _____/ \_____ _____/ \_____

| | | | | |

1C5: 145==115==195 | | | | |

165 | | | | | | |

| | | | | | | |

1C2: | | 192==152========|==============|===142 | |

| | | | | | | |

1C8: | 118=======158==168 | | | | |

| | | | | | | |

3C5: | | | 345==395==325 | | | |

| | | 365 | | | | | |

| | | | | | | | | |

3C2: | | | | | 322==352==342 | |

| | | | | | | | |

3C8: | | 368===|===398=======358 | | |

| | | | | | | |

6C2: | | | | | 642==652=======612 |

| | | | | | | |

6C8: | | 668===|==============|========658==688 | |

| | | | | | | |

6C5: | | | | | 685==615==645

| | | | | 665

|_____ _____| |_____ _____| |_____ _____|

\ / \ / \ /

5N6: 156D=====================356E=====================656F

Image Thumbs

Fata Morgana, Loop 2

FML2 42 Nodes, Rank mixed:

14 Sets = {136r3 136r7 136c2 136c8 5n46}

21 Links = {136r5 136c4 136c6 3n46 4n2 6n8 7n46 36b1 1b3 1b7 36b9}

--> (6b1) => r1c3<>6, (3b1) => r2c1<>3, (6r5) => r5c3<>6,

(3r5) => r5c7<>3, (6b9) => r8c9<>6, (3b9) => r9c7<>3

5N4: 154G=================================354H===============================================654I

/ \ ___/ \___ ___/ \__

| | | | | |

1R3: 136D=134A==|===139=======================|=========|=======================134A=136D | |

| | | | | | | | | |

1C8: | | 158==118=======================|=========|========168 | | | |

| | | | | | | | | |

1C2: | | 152=================192========|=========|===142 | | | | |

| | | | | | | | | | | |

1R7: 176P=174M==|========174M=176P=171 | | | | | | | |

| | | | | | | | | | | |

3C8: | | | | 398==358========|====|===368 | | | |

| | | | | | | | | | | | |

3R7: | | 374N=376Q======377===|===376Q=374N | | | | | |

| | | | | | | | | | | | |

3R3: | | | | | 336E=334B==|====|===331=======334B=336E | |

| | | | | | | | | | | | |

3C2: | | | | 352===|========342===|===322 | | | |

| | | | | | | | | | | |

6R3: | | | | | | | | 633==634C=636F=======|===636F=634C

| | | | | | | | | | | |

6C8: | | | | | | | 668========|=============688==658 | |

| | | | | | | | | | | |

6C2: | | | | | | 642============612=============|===652 | |

| | | | | | | | | |

6R7: | | 674O=676R============|====|======================================679===|===676R=674O

|__ ___| | | | |

\ / \ / \ /

5N6: 156J==================================356K==============================================656L

Image Thumbs

Coloin-04/13-1414, Loop 1

COL1 51 Nodes, Rank 0:

17 Sets = {167r2 167r8 1267c2 1267c8 5n6 2b28}

17 Links = {2r3 127r5 2r9 2n56 4n8 6n2 8n45 7b1 16b3 16b7 7b9}

--> (7b1) => r1c3<>7, (2n5) => r2c5<>3, (2n5) => r2c5<>8, (2n6) => r2c6<>3,

(2r3) => r3c1<>2, (4n8) => r4c8<>9, (2r5) => r5c1<>2, (1r5) => r5c3<>1,

(7r5) => r5c3<>7, (1r5) => r5c4<>1, (2r5) => r5c4<>2, (7r5) => r5c4<>7,

(1r5) => r5c7<>1, (2r5) => r5c7<>2, (7r5) => r5c9<>7, (7b9) => r7c9<>7,

(8n4) => r8c4<>5, (8n5) => r8c5<>4, (2r9) => r9c7<>2

1R8: 185==184============183

| | |

1C2: | | 172=======162============152

| | | |

1C8: | | | 158==148============138

| | | | | |

1R2: | | | | | 127=======126==125

2B8: 285==284=======294 | | | | |

| | 295 | | | | |

| | 296 | | | | |

| | | | | | | |

2C8: | | 298=============|========258===|===248 | |

| | | | | | | |

5N6: | | | 756==256==156 | | |

| | | | | | | |

2C2: | | 262===|===252========|========232 | |

| | | | | | | |

2B2: | | | | | 234============226==225

| | | | | 235 | |

6R8: | 684=================681 | | | | |

| | | | | | | |

6C2: | | 692==662 | | | |

6C8: | | | | 648==618 | |

| | | | | | | |

6R2: | | | | | 629=================626 |

7R8: 785==784==789 | | | | |

| | | | | |

7C2: | 762==752=============|==================712 | |

| | | | | |

7C8: 778======================758============748 | | |

| | |

7R2: 723==726==725

Image Thumbs

Coloin-04/13-1414, Loop 2

COL2 54 Nodes, Rank 0:

16 Sets = {1r28 2r28 6r2468 17c2 17c8 2b46 7b28}

16 Links = {7r17 26c1 2c7 6c9 2n56 4n8 5n28 6n2 8n45 1b37}

--> (7r1) => r1c3<>7, (2n5) => r2c5<>3, (2n5) => r2c5<>8, (2n6) => r2c6<>3,

(2c1) => r3c1<>2, (4n8) => r4c8<>9, (5n2) => r5c2<>4, (5n2) => r5c2<>8,

(5n8) => r5c8<>3, (5n8) => r5c8<>9, (7r7) => r7c9<>7, (8n4) => r8c4<>5,

(8n5) => r8c5<>4, (2c7) => r9c7<>2

7B2: 726=======725===============================================714

| | 715

| | 716

2R2: 226=======225==========================================221 |

| | | |

1R2: 126==127==125 | |

7C2: | | | 712==752=======762

| | | | |

2B4: | | 241=======252=======262

| | 251 | |

| | 261 | |

1C2: | | 152==172==162

2R8: | | 287============284==285 | |

| | | | | | |

7B8: | | | 774=======784==785 | |

| | | 775 | | | |

| | | 776 | | | |

| | | | | | | |

2B6: | | 258==248=======247 | | | | |

| | | | 257 | | | | |

| | | | 267 | | | | |

| | | | | | | | |

7C8: | | 758==748============778 | | | |

1R8: | | | | 184==185=================183 |

| | | | | |

6R8: | | | | 681==684 |

| | | | | |

6R6: | | | | 669============661================================662

| | | | | |

6R4: | | | 648==649============641

| | | | |

1C8: | 138=======158==148 |

| |

6R2: 626======================629

Image Thumbs

StrmCkr's Puzzle, Loop1A

ST1A 44 Nodes, Rank 0:

16 Sets = {3589r2 3589r8 3589c2 3589c8}

16 Links = {2n56 4n8 5n28 6n2 8n45 39b1 58b3 58b7 39b9}

--> (2n5) => r2c5<>4, (2n5) => r2c5<>6, (4n8) => r4c8<>6, (5n2) => r5c2<>1,

(5n2) => r5c2<>7, (5n8) => r5c8<>4, (5n8) => r5c8<>6, (8n5) => r8c5<>1,

(8n5) => r8c5<>7

5R8: 583==========================================584

| |

8R8: | 881======================885==884

| | | |

5C2: 562===========================572 | | |

| | | |

8C2: 862==852=====================================892 | |

| | | |

9C2: 962==952=======932 | |

| | | | |

3C2: 362==352==312 | | |

9R2: | 923==925==926 | |

| | | | |

3R2: 321=======325==326 | |

5C8: | | 538============548 | |

| | | | | |

8C8: | | | 818=======848==858 | |

| | | | | | | |

5R2: | 526=======527 | | | | |

| | | | | | |

8R2: 825==826============829 | | | |

9C8: 948==958=======978 | |

| | | | |

3C8: 348==358==398 | | |

| | | |

9R8: | 987==985==984

| | |

3R8: 389=======385==384

Image Thumbs

StrmCkr's Puzzle, Loop1B

ST1B 48 Nodes, Rank 0:

12 Sets = {7r79 1467b1 46b3 1b7 146b9}

12 Links = {46r2 1r8 17c2 46c8 1n3 3n1 7n9 9n7 7b8}

--> (4r2) => r2c5<>4, (6r2) => r2c5<>6, (6c8) => r4c8<>6, (1c2) => r5c2<>1,

(7c2) => r5c2<>7, (4c8) => r5c8<>4, (6c8) => r5c8<>6, (1r8) => r8c5<>1,

(7b8) => r8c5<>7

1B1: 113==131==112

| | 132

| | |

1B7: | | 172============181

| | 192 183

| | |

1B9: | | 187======================197==179

| | 189 | |

4B1: 413==431=======421 | |

| | 423 | |

| | | | |

4B3: | | 427============418 | |

| | 429 438 | |

| | | | |

4B9: | | 478=================497==479

| | 498 | |

6B1: 613==631============621 | |

| | 623 | |

| | | | |

6B3: | | 627============618 | |

| | 629 638 | |

| | | | |

6B9: | | 678============697==679

| | 698 | |

7B1: 713==731================================712 | |

732 | |

| | |

7R9: 792==795==797 |

| 796 |

| | |

7R7: 772==775=======779

776

Image Thumbs

StrmCkr's Puzzle, Cool Move

STCM 27 Nodes, Rank 0:

7 Sets = {2n5 5n28 8n5 389b5}

7 Links = {389r5 389c5 4n4}

--> (3c5) => r1c5<>3, (8c5) => r1c5<>8, (9c5) => r3c5<>9, (3r5) => r5c1<>3,

(8r5) => r5c1<>8, (9r5) => r5c3<>9, (9r5) => r5c7<>9, (3r5) => r5c9<>3,

(8r5) => r5c9<>8, (9c5) => r7c5<>9, (3c5) => r9c5<>3, (8c5) => r9c5<>8

8B5: 844============845==854

| 865 856

| | |

2N5: | 325==825===|========925

| | | | |

8N5: | 385==885===|========985

| | | |

3B5: 344==354==345 | |

| 356 365 | |

| | | |

5N2: | 352============852==952 |

| | | | |

5N8: | 358============858==958 |

| | |

9B5: 944======================954==945

956 965

Image Thumbs